( ESNUG 505 Item 6 ) -------------------------------------------- [05/24/12]
From: Trent McConaghy <trentmc=user domain=solidodesign not mom>
Subject: Solido brainiac defends Jim Hogan's earlier 6 sigma yield claims
Hi John,
I appreciate Doubting Thomas' and Curious George's interest in Jim Hogan's
letter regarding Solido High-Sigma Monte Carlo (HSMC) in ESNUG 502 #8.
I would like to respond to some of their specific concerns.
From ESNUG 503 #7:
> How can the tool guarantee "5 or 6 sigma" when the underlying SPICE
> simulator cannot? The answer they give is they assume the simulator
> is perfect, shows a fundamental gap in reasoning and a need for remedial
> statistics classes.
>
> SPICE models of physical effects are, at best, models. Even with 3D
> extraction, approximations of geometries are used. Real etched wafers
> have warped, smoothed uneven shapes and edges. At best, with first-order
> and second-order effects taken into consideration, device models will
> get within 2% or 3% of real silicon; nothing near the 99.99966% Solido
> needs to be 6 sigma.
I would first like to clarify that Jim did not state that the "simulator
is perfect", nor did he "guarantee 5 or 6 sigma".
Jim's claim for Solido HSMC is that is has "the same accuracy as millions
or billions of Monte Carlo SPICE simulations but with a low computational
cost." HSMC's accuracy depends on the accuracy of the SPICE simulations
and the MOS models -- and that's ok!
Simulating 1 million Monte Carlo (MC) samples takes too long. Simulating
1 billion MC samples? Not even possible! HSMC makes it possible to
actually *analyze* millions to billions of MC samples while only having
to simulate a few thousand -- the ones at the tails. That's the essence
of HSMC's value.
SPICE itself is not statistical, but the parameters of device models used
by SPICE may be statistical.
- SPICE solves a set of deterministic differential equations. The
numbers to construct those differential equations include values
for MOS models, which include values for process variables. To do
a SPICE simulation, a value for each process variable is set. There
are no statistics in the SPICE problem formulation. Mathematically,
in the context of HSMC, SPICE can be viewed as a deterministic
function, mapping from a vector of real-valued process variables
to a real-valued scalar output.
- SPICE uses device models, and these device models may have variables
that are characterized by a joint probability distribution. These
are the so-called "statistical MOS models".
Regarding "SPICE models of physical effects are, at best, models" - we
wholeheartedly agree. Everything's a model, unless you're working with
silicon.
MOS models are statistical, not some pie-in-the-sky estimate of a perfect
device. The MOS model statistical distribution is typically estimated
using physically-based techniques like Back-Propagation of Variance (BPV).
With BPV and other techniques, these statistical models are calibrated to
account for uneven geometries, first- and second- order effects.
As with other models, statistical MOS models don't need to be 100% accurate.
(Models are never perfect!) But, they must be systematically predictive;
an improvement in predicted yield should correspond to an improvement in
measured yield, even if there is a systematic offset between predicted and
actual yield.
Traditionally, BPV models have not been characterized out to 6 sigma, but
since they are physically-based, they extrapolate gracefully. Now that
Solido's HSMC has established itself as a means to be able to measure
circuits out to 6 sigma, we have seen as increased effort by foundries and
IDMs to further improve model accuracy at 6 sigma. For competitive
reasons, the foundries and IDMs don't publish much on this sort of work,
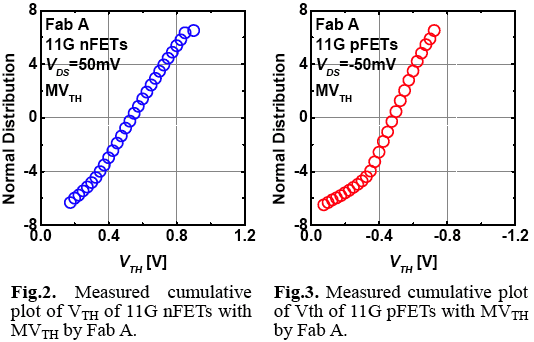
but academia does, for example: T. Mizutani, A. Kumar, and T. Hiramoto,
"Measuring threshold voltage variability of 10G transistors," Proc. IEDM,
2011. The authors of that work analyzed billions of devices on silicon,
which therefore gives accuracy to 6-sigma. They found that the threshold
voltage in nFETs roughly follows the normal distribution up to +/- 6 sigma
while pFETs have a tail in the low threshold voltage region. See the
cumulative distribution plots below.
> Solido claims their HSMC tool gets 6 sigma accuracy, which is 99.99966%,
> or 3.4 defects per million.
This requires a disambiguation. There are really two ways that the label
"6 sigma" is defined: the "The 6 Sigma Methodology" movement started by
Motorola, and 6 sigma's actual mathematical meaning.
"The 6 Sigma Methodology" uses an overly optimistic estimate of yield.
It actually shifts the true sigma value by 1.5, because promoters of the
movement basically couldn't get their designs to stay at 6 sigma.
"99.99966% yield" or "3.4 defects per million" is actually 4.5 sigma.
When Solido refers to "6 sigma", we mean in the pure mathematical sense,
without the shift. Specifically, (single-tailed) 6 sigma means yield of
99.999999901%; or a probability of failure of 9.866e-10; about 1 failure
in a billion as Jim described.
> SPICE simulations are not computed with infinite accuracy on a computer.
> They typically involve floating point numbers of maybe 6 or 8 significant
> digits. Do the 5 billion SPICE runs Solido claims and they will again be
> nowhere near the 99.99966% needed to be 6 sigma.
That SPICE simulations are only run to 6 to 8 significant digits is not an
issue. This is because from the perspective of the SPICE solver, doing
6-sigma analysis is not a big change from doing 3-sigma analysis. The
orders of magnitudes of values it sees are all approximately the same.
SPICE solves deterministic differential equations: given a netlist with a
fixed set of values for process variables, it converges to a fixed
solution. The probability density of points in process variable space is
not a determining factor.
The numeric values that SPICE has to deal with do not change by orders of
magnitude; they only change by 2x to 4x.
- In doing 3-sigma analysis, process variables in MOS models will take
values typically between 0 and 3 standard deviations from nominal, and
the output will have a particular range, call it "range A".
- In doing 6-sigma analysis, process variables will take values
typically between 0 and 3 standard deviations from nominal, and the
odd value will be out at 4 to 6 standard deviations from nominal. The
output values will have a range that is typically 1.5x to 4x of
"range A", depending on the circuit.
Since the numeric values that SPICE has to deal with do not change by orders
of magnitude, but instead by 2x to 4x, SPICE does not need dramatic new
tolerance levels -- its current settings work just fine for 6 sigma.
There is clear evidence of this in any given run of HSMC. If HSMC somehow
needed SPICE to have crazy new tolerances, the output distribution tails
found by HSMC would look like noise (unstructured) due to non-convergence
issues. But they're not - they are predictably smooth, with the odd
discontinuity.
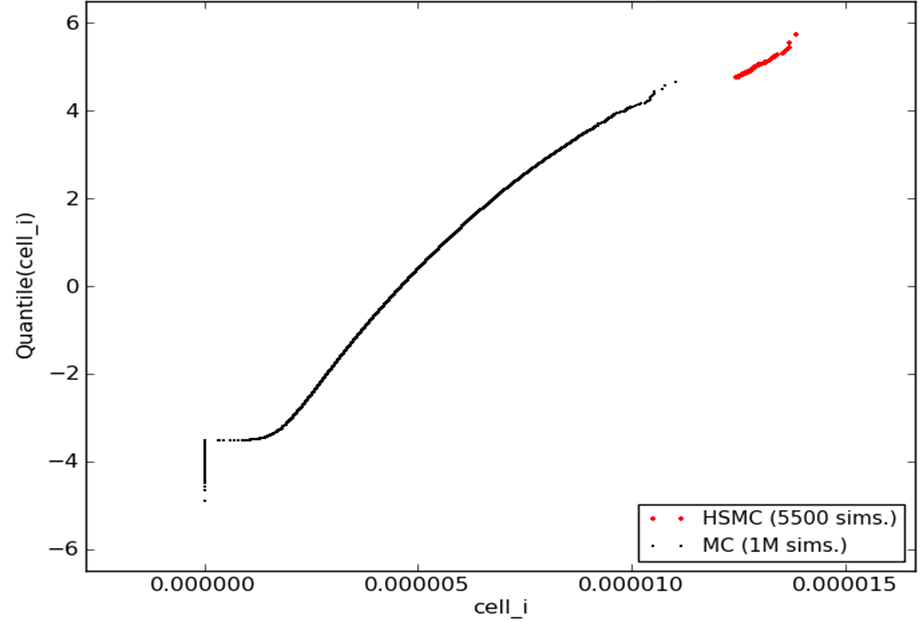
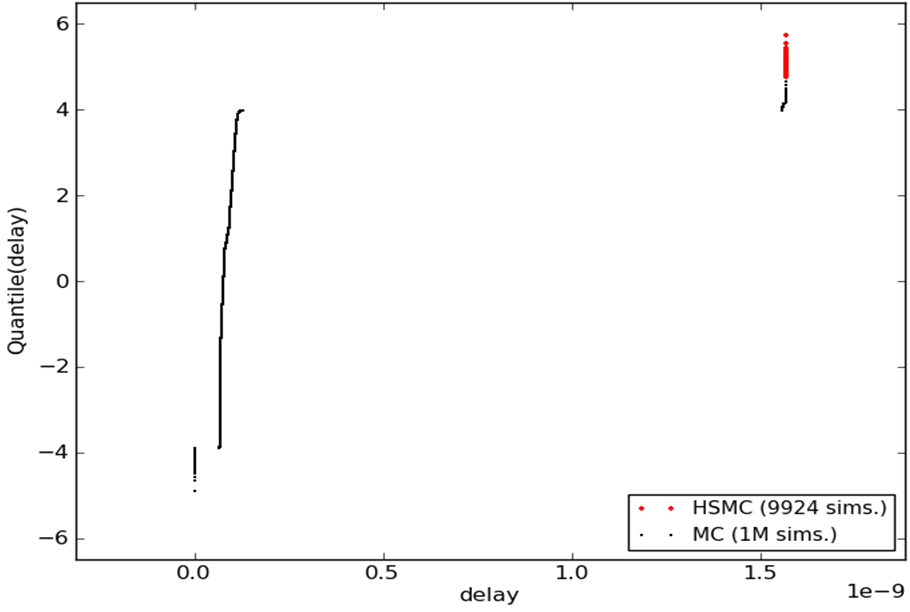
The two figures below illustrate: the figure on the top is the NQ plot for
bitcell read current, and the figure on the bottom is for a sense amp
delay. The black dots are from 1M simulated Monte Carlo samples. The red
dots are from 100 M generated Monte Carlo samples, with <10 K simulations.
In both plots, note how the black or red curves have smoothness or the odd
discontinuity, which reaffirms that there is structure to the probability
density function, and therefore structure to the mapping from process
variables to output.
You can also see from the plots that that HSMC only took 10K simulations to
do what would take 100 million simulations using traditional Monte Carlo!
Interestingly, unsigned 32-bit integers only count as high as 4.2 billion;
therefore HSMC takes special care, by using long integers. Similarly,
single-precision floating point is insufficient for computing yield from
5 billion samples, so HSMC uses double-precision. These were easy to solve
software engineering issues, versus requiring "infinite precision".
The bottom line is that you can analyze 6 sigma today with our Solido High
Sigma Monte Carlo product, using physically-based statistical MOS models
such as BPV. In fact, we have 7 companies doing it already. As Jim Hogan
stated, memory designers are the big drivers of this.
- Trent McConaghy
Solido Design Saskatoon, Canada
Join
Index
Next->Item
|
|
